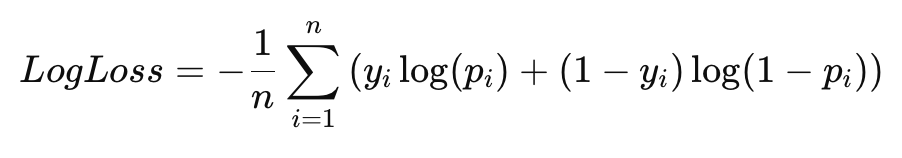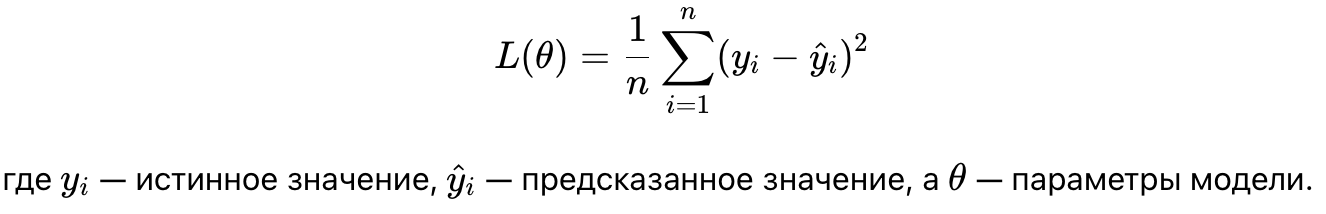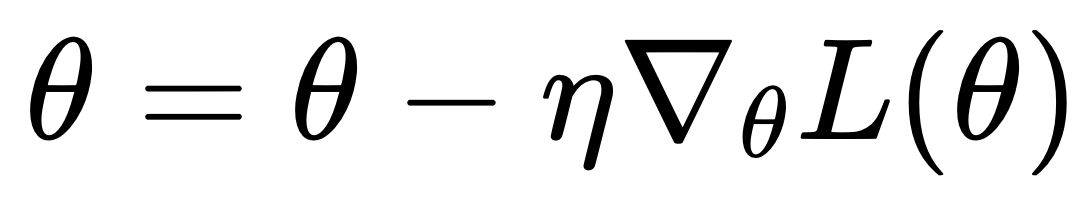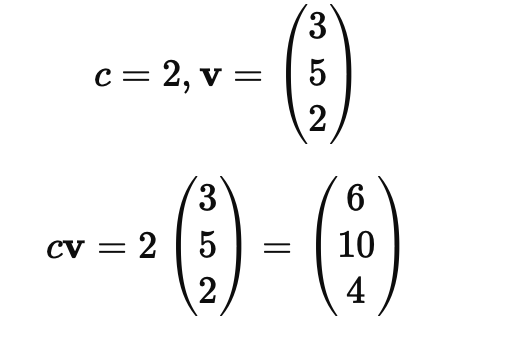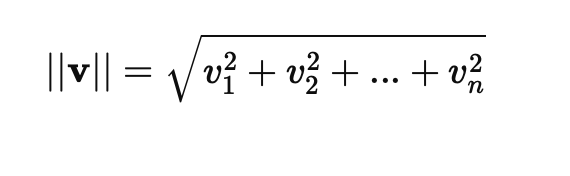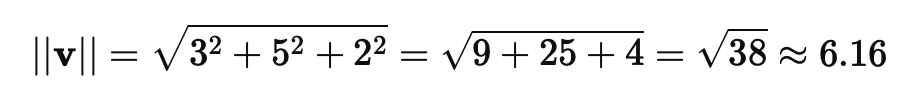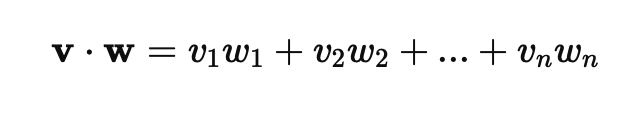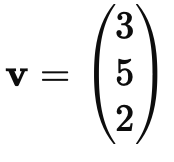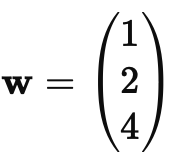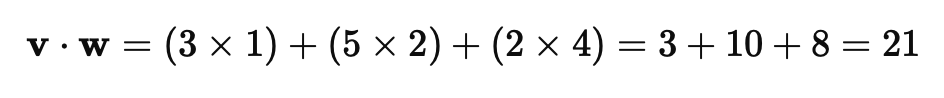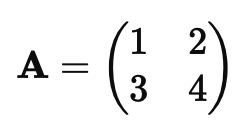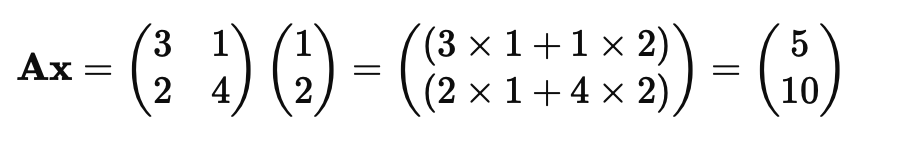Нейронные сети — это основа глубинного обучения и один из самых мощных инструментов машинного обучения, способных решать сложные задачи, такие как распознавание изображений, обработка естественного языка и прогнозирование временных рядов. Нейронные сети вдохновлены биологическими процессами в мозге и работают по принципу взаимосвязанных искусственных нейронов, которые обрабатывают информацию. В этом материале мы рассмотрим основные концепции нейронных сетей, их архитектуры, процесс обучения, и как они применяются на практике.
Что такое нейронные сети?
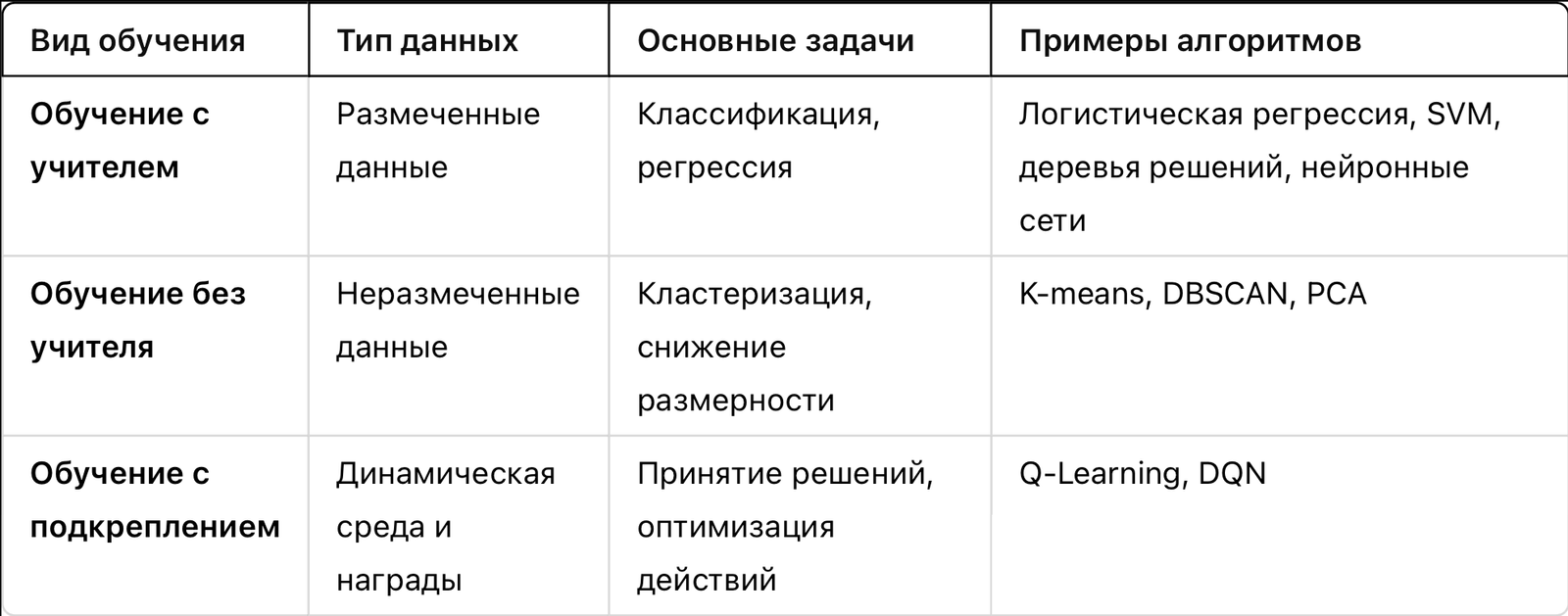
Нейронные сети — это многослойные структуры, состоящие из искусственных нейронов, которые могут обучаться находить паттерны в данных. Они могут решать задачи классификации, регрессии и другие сложные задачи, используя иерархическую структуру слоев.
Структура нейронной сети
Нейронная сеть обычно состоит из трех типов слоев:
- Входной слой: Это слой, который принимает исходные данные. Количество нейронов в этом слое соответствует количеству признаков в данных.
- Скрытые слои (hidden layers): Эти слои находятся между входным и выходным. Скрытые слои выполняют обработку данных, выявляя скрытые зависимости и паттерны. Нейронные сети могут иметь несколько скрытых слоев, что делает их «глубокими».
- Выходной слой: Это последний слой, который производит предсказания модели. В задачах классификации выходной слой может содержать нейроны, соответствующие числу классов, а в задачах регрессии — один нейрон для предсказания числового значения.
Искусственный нейрон
Искусственный нейрон — это основная вычислительная единица нейронной сети. Каждый нейрон получает несколько входов, умножает их на соответствующие веса и передает через активационную функцию.
Формула работы нейрона:

Пример работы искусственного нейрона:
import numpy as np
# Функция работы одного нейрона
def neuron(x, w, b):
return np.dot(x, w) + b
# Входные данные
x = np.array([0.5, 0.2, 0.1])
w = np.array([0.4, 0.6, 0.8])
b = 0.1
# Вычисление выхода нейрона
output = neuron(x, w, b)
print(f"Выход нейрона: {output}")
Активационные функции
Активационная функция определяет, будет ли нейрон активирован, т.е. передаст ли он сигнал дальше по сети. Активационные функции помогают моделям справляться с нелинейными зависимостями, что делает нейронные сети способными решать сложные задачи.
Наиболее распространенные активационные функции:
Сигмоидная функция (Sigmoid): Преобразует любое входное значение в диапазон от 0 до 1. Применяется в задачах бинарной классификации.
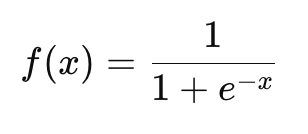
ReLU (Rectified Linear Unit): Одна из самых популярных функций, которая возвращает 0 для отрицательных значений и само значение для положительных. Она часто используется в скрытых слоях глубоких сетей.
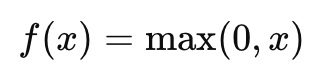
Softmax: Преобразует набор выходов в вероятности, которые суммируются до 1. Часто используется в многоклассовой классификации.
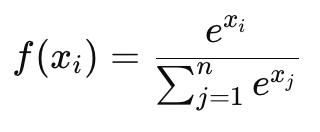
Пример использования активационной функции ReLU:
def relu(x):
return np.maximum(0, x)
# Пример использования
x = np.array([-2, -1, 0, 1, 2])
print(f"ReLU активация: {relu(x)}")
Процесс обучения нейронной сети
Прямое распространение (Forward Propagation)
Прямое распространение — это процесс, при котором данные передаются от входного слоя через скрытые слои к выходному. Каждый слой обрабатывает входные данные, применяет веса и активационные функции, после чего передает их на следующий слой, пока не будет получен окончательный результат.
Пример прямого распространения в одном слое:
def forward_propagation(X, W, b):
Z = np.dot(X, W) + b # Взвешенная сумма
A = relu(Z) # Применение активационной функции
return A
Функция ошибки
Функция ошибки (или функция потерь) измеряет, насколько предсказания модели отклоняются от реальных значений. Основная задача обучения нейронной сети — минимизировать ошибку.
MSE (Mean Squared Error) для задач регрессии:

Cross-Entropy (Перекрестная энтропия) для задач классификации:
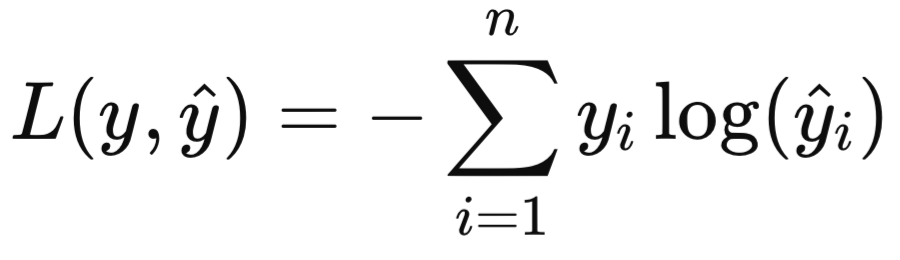
Обратное распространение (Backpropagation)
Обратное распространение — это ключевой процесс обновления весов в сети на основе ошибки, полученной на выходе. Для этого используется метод градиентного спуска, который корректирует веса нейронов для минимизации ошибки.
Градиентный спуск вычисляет, как сильно вес влияет на ошибку, и затем обновляет его в направлении, которое минимизирует ошибку:
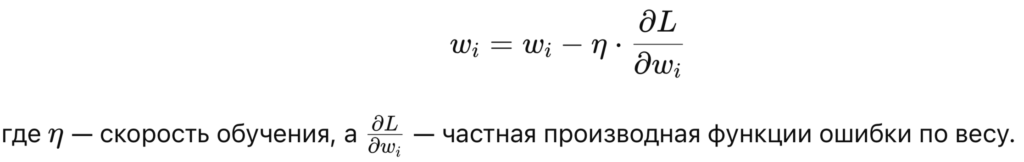
Варианты градиентного спуска
Для ускорения и стабилизации процесса обучения существуют разные варианты градиентного спуска:
- Стохастический градиентный спуск (SGD): Обновляет веса после каждого примера в тренировочном наборе данных. Это ускоряет обучение, но может быть нестабильным.
- Mini-batch SGD: Разделяет данные на небольшие пакеты (batch), и обновляет веса после обработки каждого пакета, что делает обучение более стабильным.
- Adam: Популярный оптимизатор, который комбинирует преимущества SGD и других методов, таких как RMSProp, и часто дает более стабильные и быстрые результаты.
Архитектуры нейронных сетей
Полносвязные сети (Fully Connected Networks)
Полносвязные сети — это базовая архитектура нейронных сетей, где каждый нейрон одного слоя связан со всеми нейронами следующего слоя. Такие сети используются для задач классификации и регрессии, когда нет пространственных или временных зависимостей в данных.
Сверточные нейронные сети (Convolutional Neural Networks, CNN)
Сверточные сети особенно эффективны для анализа изображений и видео. В сверточных сетях используются сверточные слои, которые вылавливают особенности изображений (например, границы, текстуры). Эти сети способны обрабатывать пространственные данные и находить паттерны, такие как объекты на изображении.
Основные компоненты CNN:
- Сверточный слой: Выполняет свертку (convolution) изображения с набором фильтров для извлечения признаков.
- Пуллинг (Pooling): Уменьшает размерность данных, сохраняя важную информацию.
- Полносвязный слой: Завершающий этап, который преобразует извлеченные признаки в выходное предсказание.
Рекуррентные нейронные сети (Recurrent Neural Networks, RNN)
Рекуррентные нейронные сети особенно полезны для работы с последовательными данными, такими как текст, временные ряды и аудио. В RNN информация передается не только вперед, но и назад по сети, что позволяет учитывать предшествующие элементы последовательности при предсказании следующих.
Однако стандартные RNN имеют проблемы с долгосрочной зависимостью. Для их решения были созданы улучшенные модели, такие как:
- LSTM (Long Short-Term Memory): Умеет «запоминать» важную информацию на длительных интервалах времени.
- GRU (Gated Recurrent Unit): Упрощенная версия LSTM, которая также хорошо работает с последовательными данными, но использует меньше вычислительных ресурсов.
Регуляризация в нейронных сетях
Регуляризация помогает предотвратить переобучение (overfitting), когда модель слишком сильно адаптируется к тренировочным данным и не обобщает их на новые данные. Наиболее популярные методы регуляризации:
- Dropout: В процессе обучения случайно «выключает» нейроны, что предотвращает слишком сильную зависимость от отдельных нейронов и делает модель более устойчивой.
- L2-регуляризация: Добавляет штраф за слишком большие веса нейронов, что помогает сделать модель менее сложной.
Пример применения Dropout в Python:
from tensorflow.keras.layers import Dropout # Пример слоя с Dropout model.add(Dropout(0.5)) # 50% нейронов отключаются случайным образом
Применение нейронных сетей
Нейронные сети применяются в самых разных областях:
- Компьютерное зрение: Распознавание объектов, классификация изображений, сегментация изображений.
- Обработка естественного языка: Анализ тональности текста, машинный перевод, чат-боты.
- Распознавание речи: Преобразование речи в текст и наоборот.
- Временные ряды и прогнозирование: Прогнозирование спроса, экономических показателей, анализ временных рядов.
Оценка и тестирование моделей
Для оценки производительности моделей нейронных сетей необходимо разделять данные на тренировочную и тестовую выборки. Это помогает проверить, как хорошо модель будет работать на новых данных.
Пример визуализации обучения:
import matplotlib.pyplot as plt
# Визуализация потерь на обучающей и тестовой выборке
plt.plot(history.history['loss'], label='Training Loss')
plt.plot(history.history['val_loss'], label='Validation Loss')
plt.title('График обучения')
plt.xlabel('Эпохи')
plt.ylabel('Потери')
plt.legend()
plt.show()
Заключение
Нейронные сети — это мощный инструмент машинного обучения, способный решать сложные задачи в самых разных областях. Правильное понимание структуры, процессов обучения и архитектур нейронных сетей позволяет создавать эффективные модели для обработки изображений, текста и временных рядов. Глубокое обучение развивается стремительными темпами, и его применение открывает новые возможности для анализа данных и автоматизации задач.
Рекомендации для самостоятельного изучения:
- Книга «Deep Learning» от Ian Goodfellow.
- Онлайн-курсы по глубокому обучению на Coursera (DeepLearning.ai).
- Практические задачи по глубокому обучению на Kaggle.