Статистика и теория вероятностей играют ключевую роль в методах искусственного интеллекта (AI) и машинного обучения. Эти дисциплины позволяют анализировать данные, выявлять закономерности и предсказывать будущие события на основе наблюдений. В этой лекции мы рассмотрим основные понятия статистики и вероятностей, углубимся в их применение в AI, а также покажем примеры кода и задач для практической работы.
1. Основные понятия статистики
1.1 Выборка и генеральная совокупность
- Генеральная совокупность: Полный набор объектов или событий, которые нас интересуют. Примером может быть вся популяция людей в стране или все транзакции на платформе.
- Выборка: Подмножество генеральной совокупности, которое используется для анализа. Это важно, потому что часто работа с полной совокупностью невозможна из-за её объема.
Пример: Если генеральная совокупность — это все пользователи сайта, то выборка может быть набор данных о 10 000 случайных пользователях, которые представляют всю совокупность.
1.2 Описательные статистики
- Среднее (математическое ожидание): Среднее значение выборки. Используется для определения центра данных.
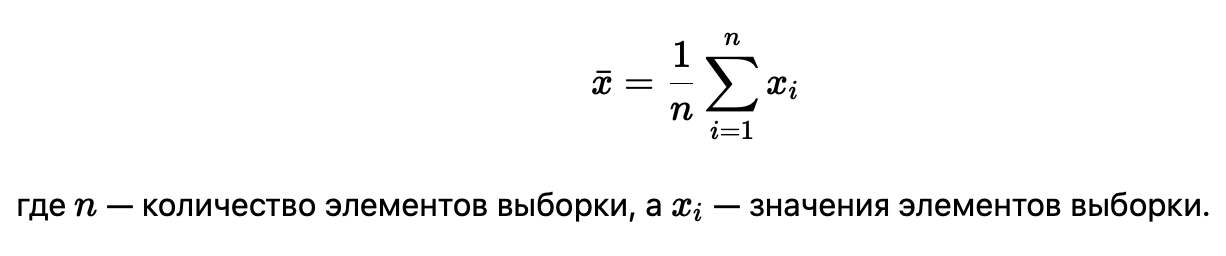
- Медиана: Значение, которое делит данные пополам. Медиана устойчива к выбросам, что делает её полезной, когда данные содержат экстремальные значения.
- Дисперсия и стандартное отклонение: Эти показатели измеряют разброс данных относительно среднего. Дисперсия показывает отклонение данных от среднего, а стандартное отклонение — это его квадратный корень.
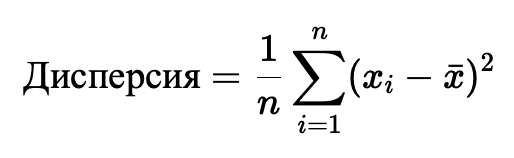
Пример: Средний доход пользователей можно использовать для анализа покупательской способности, а стандартное отклонение покажет, насколько доходы пользователей варьируются относительно среднего.
1.3 Корреляция и ковариация
- Корреляция: Показывает степень взаимосвязи между двумя переменными. Значение корреляции варьируется от -1 до 1. Корреляция 1 указывает на сильную положительную связь, -1 — на сильную отрицательную связь.

- Ковариация: Измеряет, как изменяются две переменные относительно друг друга. Если ковариация положительная, переменные растут вместе; если отрицательная — одна переменная уменьшается, когда другая растёт.
Пример: Корреляция между маркетинговыми расходами и продажами может быть использована для определения эффективности рекламных кампаний.
1.4 Распределения
Распределение данных показывает, как значения распределены по диапазону.
- Нормальное распределение: Симметричное распределение вокруг среднего значения. Применяется в задачах линейной регрессии и анализе ошибок моделей.
- Биномиальное распределение: Описывает вероятность достижения определенного числа успехов в серии независимых испытаний (например, подбрасывание монеты).
- Экспоненциальное распределение: Описывает вероятности времени до наступления следующего события (например, время до поломки оборудования).
2. Основные понятия теории вероятностей
2.1 Вероятность
Вероятность — это мера того, насколько вероятно наступление события. Вероятности выражаются в диапазоне от 0 (событие никогда не происходит) до 1 (событие произойдет с полной уверенностью).

Пример: Вероятность выпадения «орла» при подбрасывании монеты равна 0.5, поскольку у монеты два равновероятных исхода.
2.2 Условная вероятность
Условная вероятность — это вероятность события A, при условии, что событие B уже произошло. Используется для прогнозирования, когда известны определённые условия.
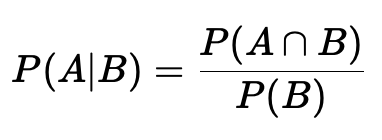
Пример: Вероятность того, что пользователь совершит покупку (A), если он уже добавил товар в корзину (B).
2.3 Теорема Байеса
Теорема Байеса позволяет пересчитывать вероятность события, исходя из новой информации. Она широко применяется в задачах классификации и диагностики.
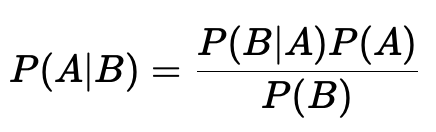
Пример: Если пациент получил положительный результат теста на заболевание (B), теорема Байеса помогает оценить вероятность того, что он действительно болен (A), исходя из частоты заболевания в популяции и точности теста.
Практический пример в Python:
# Пример применения теоремы Байеса
def bayesian_probability(p_a, p_b_given_a, p_b):
return (p_b_given_a * p_a) / p_b
# Допустим, вероятность болезни (P(A)) = 0.01, точность теста (P(B|A)) = 0.99, вероятность положительного теста (P(B)) = 0.05
p_a = 0.01
p_b_given_a = 0.99
p_b = 0.05
result = bayesian_probability(p_a, p_b_given_a, p_b)
print(f"Вероятность, что пациент действительно болен при положительном тесте: {result:.4f}")
3. Применение статистики и вероятностей в AI
3.1 Машинное обучение
- Логистическая регрессия: Вероятностная модель, которая предсказывает вероятность принадлежности объекта к определенному классу. Важна для задач бинарной классификации, например, предсказания, купит ли пользователь товар.
- Наивный байесовский классификатор: Использует теорему Байеса для классификации объектов. Предполагает независимость признаков и часто применяется в задачах анализа текста.
3.2 Оценка неопределенности
В прогнозировании важно оценивать неопределенность модели. Статистические методы, такие как доверительные интервалы, позволяют определить диапазон возможных значений прогнозов.
Пример: В прогнозировании продаж важно не только знать точное число, но и вероятность того, что продажи будут находиться в определенном диапазоне.
3.3 Анализ A/B тестов
A/B тесты используются для сравнения двух версий продукта (например, двух версий веб-страницы). Статистические методы позволяют определить, является ли одно из решений лучше с учетом случайных факторов.
3.4 Регуляризация
Регуляризация — это метод, который помогает предотвратить переобучение моделей машинного обучения. Методы регуляризации (например, L2-регуляризация) используют статистические принципы для ограничения сложности модели.
4. Важные распределения в AI
4.1 Нормальное распределение
Нормальное распределение часто используется в моделях линейной регрессии и для оценки ошибок моделей. Важным аспектом является центральная предельная теорема, согласно которой сумма независимых случайных переменных с любым распределением приближается к нормальному распределению.
4.2 Биномиальное распределение
Биномиальное распределение моделирует вероятность наступления определенного числа успехов в серии независимых испытаний. Используется для задач, связанных с событиями, которые имеют два исхода (например, да/нет, успех/неудача).
Пример: Рассчитаем вероятность выпадения 5 «орлов» при 10 подбрасываниях монеты.
import scipy.stats as stats
# Вероятность выпадения 5 орлов при 10 подбрасываниях монеты (P(success) = 0.5)
prob = stats.binom.pmf(k=5, n=10, p=0.5)
print(f"Вероятность выпадения 5 орлов: {prob:.4f}")
4.3 Пуассоновское распределение
Это распределение описывает количество событий, которые происходят за фиксированный интервал времени или пространства, например, количество звонков в колл-центр за час.
Заключение
Статистика и теория вероятностей являются важнейшими инструментами для анализа данных и построения моделей в AI. Они позволяют не только анализировать данные, но и делать обоснованные прогнозы и принимать решения на основе неопределенности. Важно понимать и применять эти методы для успешного использования машинного обучения и искусственного интеллекта в реальных задачах.
Рекомендации для самостоятельного изучения:
- Гилберт Странг, «Введение в линейную алгебру».
- Онлайн-курсы по теории вероятностей и статистике на Coursera и edX.
- Лекции по статистике от MIT OpenCourseWare.

Добавить комментарий