Алгоритмы машинного обучения

Написано

Artem Kondranin

в

Алгоритмы машинного обучения — это основа для создания моделей, которые могут обучаться на данных и принимать решения. Эти алгоритмы используются для решения различных задач, таких как классификация, регрессия и кластеризация. В этом материале мы рассмотрим наиболее популярные алгоритмы машинного обучения, включая линейные модели, деревья решений, метод опорных векторов (SVM), k-ближайших соседей (kNN) и ансамблевые методы. Помимо описания каждого алгоритма, мы включим примеры их использования, графические иллюстрации и важные аспекты, такие как регуляризация и выбор гиперпараметров.

Линейные модели

Линейная регрессия

Линейная регрессия — это базовый алгоритм для решения задач регрессии. Он строит линейную зависимость между входными переменными (признаками) и целевой переменной. Цель — минимизировать разницу между реальными значениями и предсказаниями.

  • Формула линейной регрессии:
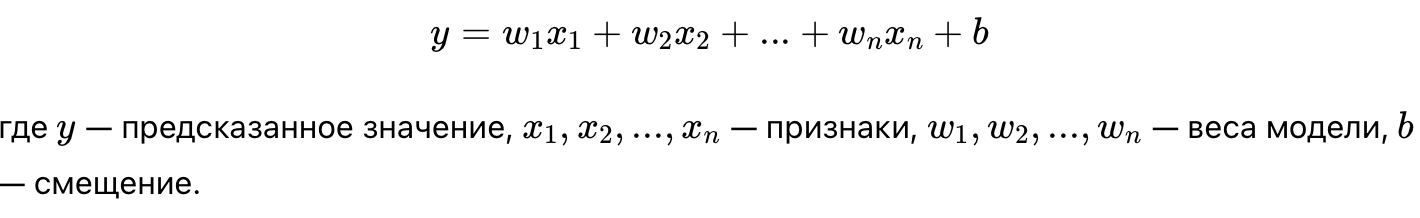
  • Применение: Линейная регрессия используется для прогнозирования непрерывных величин, таких как цены на недвижимость или уровень продаж.

Пример линейной регрессии:

from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_boston
from sklearn.metrics import mean_squared_error

# Загрузка данных (цены на жилье)
X, y = load_boston(return_X_y=True)

# Разделение данных на обучающую и тестовую выборки
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# Обучение модели линейной регрессии
model = LinearRegression()
model.fit(X_train, y_train)

# Прогнозирование и оценка
y_pred = model.predict(X_test)
print(f"Среднеквадратичная ошибка: {mean_squared_error(y_test, y_pred):.4f}")

Визуализация линейной регрессии

Для двухмерного случая линейная регрессия может быть визуализирована как прямая, проходящая через точки данных. Это помогает понять, как модель подгоняет линию под набор данных.

import numpy as np
import matplotlib.pyplot as plt

# Пример простых данных для визуализации
X = np.array([1, 2, 3, 4, 5]).reshape(-1, 1)
y = np.array([1.2, 1.9, 3.0, 3.8, 5.1])

# Обучение модели линейной регрессии
model = LinearRegression()
model.fit(X, y)

# Визуализация
plt.scatter(X, y, color='blue')
plt.plot(X, model.predict(X), color='red')
plt.title('Линейная регрессия')
plt.xlabel('X')
plt.ylabel('y')
plt.show()

Регуляризация

Регуляризация — это метод, который добавляет штраф за слишком большие веса в линейной модели, чтобы избежать переобучения. Существует два основных типа регуляризации:

  • L1-регуляризация (Lasso): Штрафует абсолютные значения весов.
  • L2-регуляризация (Ridge): Штрафует квадраты весов.

Регуляризация помогает моделям избежать переобучения на тренировочных данных и улучшить их обобщающую способность на новых данных.

Логистическая регрессия

Логистическая регрессия — это алгоритм классификации, который оценивает вероятность того, что объект принадлежит к одному из двух классов. Логистическая регрессия использует сигмоидную функцию для вывода вероятности.

  • Формула логистической регрессии:
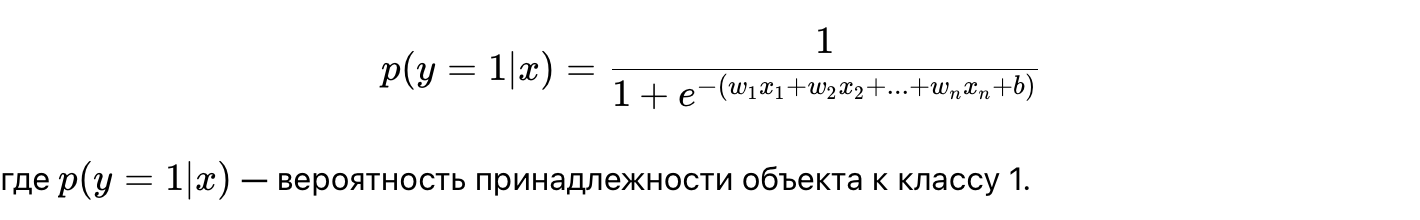
  • Применение: Логистическая регрессия используется для решения задач бинарной классификации, таких как прогнозирование того, совершит ли клиент покупку или покинет компанию.

Пример логистической регрессии:

from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_breast_cancer
from sklearn.metrics import accuracy_score

# Загрузка данных
X, y = load_breast_cancer(return_X_y=True)

# Разделение данных на обучающую и тестовую выборки
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# Обучение модели логистической регрессии
model = LogisticRegression(max_iter=10000)
model.fit(X_train, y_train)

# Прогнозирование и оценка точности
y_pred = model.predict(X_test)
print(f"Точность модели: {accuracy_score(y_test, y_pred):.4f}")

Деревья решений

Деревья решений — это алгоритм, который представляет собой древовидную структуру, где каждый узел проверяет одно из условий, а листья представляют итоговые решения или предсказания.

  • Принцип работы: Данные последовательно разбиваются на подмножества в зависимости от их признаков, с целью минимизации неопределенности или ошибки.
  • Применение: Деревья решений используются как для классификации, так и для регрессии.

Визуализация дерева решений:

Для визуализации дерева решений полезно видеть его структуру, где каждый узел представляет вопрос о данных, а ветви указывают на результат.

from sklearn.tree import DecisionTreeClassifier
from sklearn import tree
import matplotlib.pyplot as plt

# Загрузка данных и обучение модели
X, y = load_iris(return_X_y=True)
model = DecisionTreeClassifier().fit(X, y)

# Визуализация дерева
plt.figure(figsize=(10, 8))
tree.plot_tree(model, filled=True)
plt.title('Дерево решений')
plt.show()

Преимущества и недостатки деревьев решений:

Преимущества:

  • Простота в интерпретации.
  • Не требует масштабирования данных.

Недостатки:

  • Склонны к переобучению.
  • Могут быть нестабильны (небольшие изменения данных могут привести к сильно отличающимся деревьям).

Метод опорных векторов (SVM)

SVM (метод опорных векторов) — это мощный алгоритм классификации, который строит гиперплоскость для разделения данных на классы. Алгоритм пытается найти такую гиперплоскость, которая максимально отдалена от ближайших объектов каждого класса.

  • Применение: SVM используется в задачах классификации, таких как распознавание изображений, текстов и биоинформатика.

Визуализация гиперплоскости SVM:

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.svm import SVC

# Генерация данных
X, y = datasets.make_classification(n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1)

# Обучение модели SVM
model = SVC(kernel='linear')
model.fit(X, y)

# Визуализация гиперплоскости
w = model.coef_[0]
b = model.intercept_[0]
x_plot = np.linspace(min(X[:, 0]), max(X[:, 0]), 100)
y_plot = -(w[0] * x_plot + b) / w[1]

plt.scatter(X[:, 0], X[:, 1], c=y)
plt.plot(x_plot, y_plot, 'r--')
plt.title('Гиперплоскость SVM')
plt.show()

Преимущества и недостатки SVM:

Преимущества:

  • Хорошо работает на высокоразмерных данных.
  • Эффективен при линейно разделимых данных.

Недостатки:

  • Трудоемок на больших наборах данных.
  • Чувствителен к шуму и перекосам данных.

K-ближайших соседей (kNN)

k-ближайших соседей (kNN) — это алгоритм классификации, который предсказывает класс нового объекта на основе классов kk ближайших объектов в обучающей выборке. Расстояние обычно измеряется с использованием евклидова расстояния.

Пример k-ближайших соседей:

from sklearn.neighbors import KNeighborsClassifier
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

# Загрузка данных
X, y = load_iris(return_X_y=True)

# Разделение данных на обучающую и тестовую выборки
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# Обучение модели kNN
model = KNeighborsClassifier(n_neighbors=5)
model.fit(X_train, y_train)

# Оценка точности на тестовой выборке
y_pred = model.predict(X_test)
print(f"Точность модели: {accuracy_score(y_test, y_pred):.4f}")

Преимущества и недостатки kNN:

Преимущества:

  • Прост в реализации.
  • Хорошо работает на малых объемах данных.

Недостатки:

  • Медленный на больших объемах данных.
  • Чувствителен к выбору параметра kk и метрике расстояния.

Ансамблевые методы

Случайный лес (Random Forest)

Случайный лес — это ансамблевый метод, который строит множество деревьев решений на разных подмножествах данных и усредняет их предсказания. Это повышает точность модели и снижает риск переобучения.

Пример случайного леса:

from sklearn.ensemble import RandomForestClassifier

# Обучение модели случайного леса
model = RandomForestClassifier(n_estimators=100, random_state=42)
model.fit(X_train, y_train)

# Оценка точности
y_pred = model.predict(X_test)
print(f"Точность случайного леса: {accuracy_score(y_test, y_pred):.4f}")

Преимущества и недостатки:

Преимущества:

  • Высокая точность.
  • Устойчивость к переобучению.

Недостатки:

  • Требует больше вычислительных ресурсов.
  • Труднее интерпретировать.

Градиентный бустинг

Градиентный бустинг — это метод, который строит ансамбль деревьев последовательно, где каждое следующее дерево исправляет ошибки предыдущего. Это один из наиболее мощных алгоритмов для задач регрессии и классификации.

Популярная реализация градиентного бустинга — XGBoost, который широко используется на соревнованиях по машинному обучению.

Заключение

Алгоритмы машинного обучения включают как простые методы, такие как линейная регрессия и деревья решений, так и более сложные модели, такие как метод опорных векторов и ансамблевые методы. Выбор подходящего алгоритма зависит от типа задачи, объема данных и требований к производительности. Регуляризация и настройка гиперпараметров играют важную роль в создании эффективных моделей.

Рекомендации для самостоятельного изучения:

  • Книга «Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow» от Aurélien Géron.
  • Онлайн-курсы по машинному обучению на Coursera и edX.
  • Лекции по машинному обучению от MIT OpenCourseWare.

Следите за обновлениями в нашем Telegram-канале!

Чтобы не пропустить новые материалы, подписывайтесь на наш Telegram-канал. Здесь вы сможете получать все статьи, курсы и эксклюзивные материалы прямо в удобный мессенджер. А также быть в курсе последних новостей и инсайтов из мира AI.

Присоединяйтесь к сообществу единомышленников, задавайте вопросы и делитесь своим мнением — будем учиться и развиваться вместе!

Подписаться можно по ссылке: https://t.me/proaionru

Отличные новости для всех моих подписчиков! 🎉 При покупке продукции JetBrains вы можете использовать специальный промокод «Asgru24» и получить скидку 25% на любой товар! Не упустите шанс сэкономить на лучших инструментах разработки.

Комментарии

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *

Больше записей